担当: K.T (M2)
研究背景・概要
私たちの研究室は、核融合発電と呼ばれる次世代のクリーンエネルギー源の実現に向けてシミュレーションの観点から研究を行っています。研究対象となる物理系はプラズマです。プラズマは固体・液体・気体に次ぐ物質の第4の状態と言われ、気体を構成する分子が陽イオンと電子に電離している状態です。プラズマは何か特別な状態で身近なところには存在しないようなものと思えますが実はそんなことはなく、宇宙の99%はプラズマ状態にあると言われています。私たちが経験できるプラズマには例えば雷やオーロラ、太陽などがあります。核融合発電はプラズマの一つである太陽(と同じ原理のもの)を地上につくり、膨大なエネルギーを取り出そうというものです。

1-1. プラズマシミュレーションの問題
プラズマを構成する電子やイオンが従う方程式は以下の運動方程式です。
運動方程式:
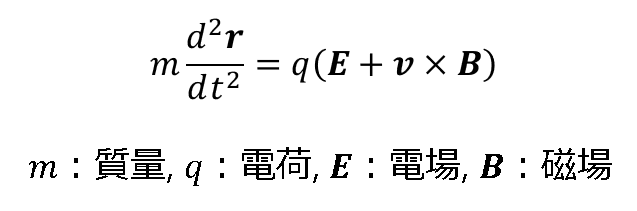
運動方程式をすべての電子とイオンについて解くことができれば、原理的にはプラズマのすべての現象を知ることができます。しかし、プラズマ中に存在するイオンや電子の個数は非常に大きく、核融合プラズマの典型的な密度は1020/m3程度にもなります。したがって、すべてをシミュレーションすることは不可能です。そこで実際には統計的な扱いや物理的な仮定をしたモデルを用いることで計算コストを抑え、シミュレーションを可能としています。しかし、そのシミュレーション結果は時に実験結果と一致しない場合があります。つまり、プラズマの数値シミュレーションでは、常に「計算コスト」を意識しつつ実験結果と一致するモデルを構築しなければなりません。
1-2. 量子コンピュータとは
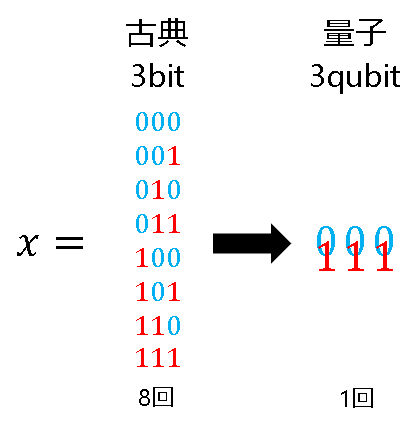
近年、量子コンピュータが世間から注目を集めています。量子コンピュータは「量子力学」の原理で動くコンピュータです。一方で私たちが普段使うようなノートパソコンや「富岳」に代表されるスパコンなどは「古典力学」の原理で動いており、量子コンピュータと比較されて「古典コンピュータ」と呼ばれます。両者の最も大きな違いは情報の表現方法です。「0~7」の8個の数字を表現するのに、古典コンピュータは3bitの数字を8回用意する必要がありますが、量子コンピュータは3qubit(qubitは古典bitの量子版)を用いれば8個分の情報を1回で表現できます。一般化すれば、n-bitの情報を表示するのに古典コンピュータでは2n回必要ですが、量子コンピュータではn-qubitを1回で済みます。この性質を「重ね合わせ」と呼び、これが量子コンピュータが古典コンピュータの性能を上回ると期待される理由です。もし100ビットを考えれば2100≒1031程度になることから、いかに量子コンピュータが強力かがわかると思います。
1-3. プラズマと量子コンピュータ
プラズマシミュレーションには非常に大きな計算コストがかかり、それが問題になっていることを上で説明しました。そして量子コンピュータは古典コンピュータと比べて計算能力が高い可能性があることも説明しました。これらを考えると量子コンピュータによってプラズマシミュレーションの計算コストの問題を改善できるのではないかと期待できます。
プラズマシミュレーションにこれまで用いられてきた古典コンピュータ(主にスパコン)を、量子コンピュータに置き換えることで、より高速な計算手法を確立し計算コストの改善を実現しようというのが私の研究です。

1-4. Vlasov-Maxwell方程式系
プラズマの時間発展を記述する基本的な方程式は、Vlasov方程式とMaxwell方程式です。プラズマ中の電子やイオンの運動をすべて考えることはできないので、分布関数というものを導入します。分布関数とはある位置、速度、時間に対する粒子の数密度を表したものです。この分布関数の時間発展を表す式がVlasov方程式です。
Vlasov方程式:
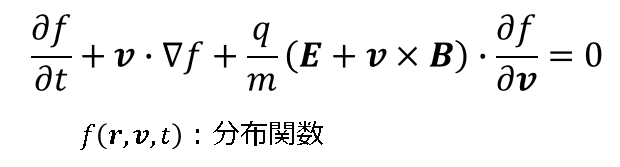
さらにプラズマの巨視的な電磁場の時間発展を表すMaxwell方程式を加えます。
Maxwell方程式:
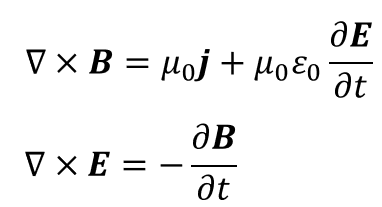
これらの方程式からなる系を「Vlasov-Maxwell方程式系」と呼び、プラズマを記述する代表的な方程式系です。Vlasov-Maxwell方程式系をシミュレーションすることは、一般に非常に計算コストがかかります。
研究方法
本研究は、Vlasov-Maxwell方程式系の量子アルゴリズム(量子コンピュータ上で動かすアルゴリズム)を開発・拡張し、Qiskit(IBM Researchが提供する量子コンピュータ用のフレームワーク)を用いてシミュレーターで計算します。言語はPythonです。自宅や研究室からリモートサーバーに接続して計算を行います。
プラズマの基本的な物理現象(線形Landau減衰など)をVlasov-Maxwell方程式系の量子アルゴリズムを用いて再現することで、プラズマシミュレーションが量子コンピュータで実行可能であるかどうかを評価し、そして何ができ何ができないのかを探索していきます。
実績
[1] K. Toyoizumi and K. Hoshino, Quantum algorithm for the Vlasov simulation of neutral gas, in The 41st JSST Annual International Conference on Simulation Technology (JSST2022).
[2] K. Toyoizumi, N. Yamamoto, and K. Hoshino, Hamiltonian simulation using quantum singular value transformation: complexity analysis and application to the linearized Vlasov-Poisson equation, arXiv:2304.08937 (2023).
3年生へ
私の研究は、プラズマと量子コンピュータを融合させた研究分野であり、まだまだ研究者もいません。なので大変なことも多いですが、一方でチャレンジングで非常に面白いと思っています。もし私自身の研究や研究室のことなどに興味や質問があれば、気軽に連絡してください。
またもし量子コンピュータを学びたい触ってみたいという方がいれば、以下のリンクで勉強してみるとよいかもしれません。
Qiskit Textbook: https://qiskit.org/textbook/ja/preface.html